直接照度の計算法 | 照明設計サポート P.L.A.M. | Panasonic

印刷はこちらから

直接照度とは

直接照度の計算方法

直接照度とは

直接照度とは、光源または照明器具からの直接光だけによって得られる照度のことです。ここでは、光源の形状別（点光源、直線光源、面光源）の直接照度について説明します。

直接照度の計算方法

1.点光源による直接照度

1つの点光源Lによる、ある面上の点Pにおける水平面照度Ehは、

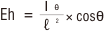
Eh＝Ⅰθ/ℓ2×cosθ

Iθ=θ方向の光度（cd）
ℓ=光源からその点までの距離（m）
θ＝入射角

図1：点光源による照度

光源と照明の関係を示す図。点Oから高さhの位置にある光源Lから点Pまでの距離はdで表され、光線が角度θで点Pに到達する様子が示されている。点Pにおける水平面での照度Eh、垂直面での照度Evφ、および法線方向の照度Enが図解されている。

【計算例１】

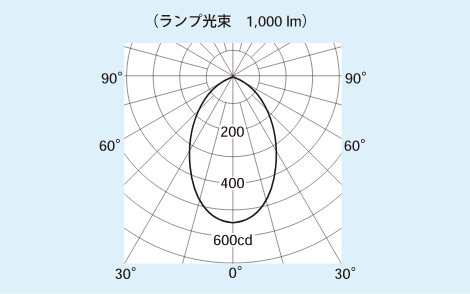
右図の配光線をもつ高天井用器具（ランプ光束30,500 lm）を使用し、作業面上7mに取り付けた場合、その直下P0の照度はいくらになりますか？

（解）この場合の計算式は、

E＝Ⅰ/ℓ2

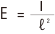
真下方向の光度Iは、配光曲線によると540cd。
ただし、これはランプ光束1,000 ｌｍとして書いてありますから、

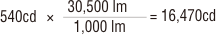
540cd×30,500lm/1,000lm＝16,470cd

故に直下の照度Eは、

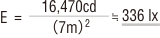
E＝16,470cd（7m）2≒336lx

となります。

図2：高天井器具の配光曲線

ランプ光束1,000 lmの配光特性を示す極座標グラフ。中心から放射状に角度が描かれ、0°、30°、60°、90°の範囲で配光が示されている。等照度線は200cd、400cd、600cdで描かれ、光束が角度に応じて分布している様子を示している。

法線照度En、水平面照度Eh、鉛直面照度Evo、Evφを、各々入射角θと、光源からその点までの距離ℓ、光源の高さh、水平距離dなどで表せば表1のようになります。

表1：点光源による直射照度

距離ℓ：En=Iθ/ℓの2乗、Eh=Iθ/ℓの2乗cosθ、Evo=Iθ/ℓの2乗sinθ、Evφ=Iθ/ℓの2乗sinθcosθ、光源の高さh：En=Iθ/hの2乗cosの2乗θ、Eh=Iθ/hの2乗cosの3乗θ、Evo=Iθ/hの2乗sinθcosの2乗θ、Evφ=Iθ/hの2乗sinθcosの2乗θcosφ、水平距離d：En=Iθ/dの2乗sinの2乗θ、Eh=Iθ/dの2乗sinの2乗θcosθ、Evo=Iθ/dの2乗sinの3乗θ、Evφ=Iθ/dの2乗sinの3乗θcosφ、EnX：En=1、Eh=cosθ、Evo=sinθ、Evφ=sinθcosφ

【計算例２】

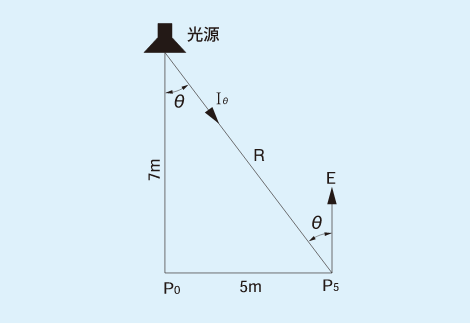
計算例1で、真下P0より横に5m離れた点P5の水平面照度はいくらになりますか？

（解）光が斜めに入射する場合の計算式は

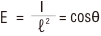
E＝Ⅰ/ℓ2＝cosθ

光源より点P5の方向の鉛直角θは、

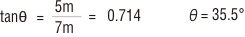
tanθ＝5m/7m＝0.714　θ＝35.5°

※θ=35.5°方向の光度Iは、配光曲線によると300cd。
（作図で求めてもよいし、下のように計算してもよい）
したがって、θ方向の光線Iθは、

ℓ²=7²+5²=74

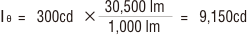
ℓ2＝7の2乗＋5の2乗＝74、Ⅰθ＝300cd×30,500lm/1,000lm＝9,150cd

故に点P5の照度は

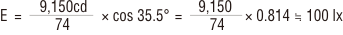
E＝9,150cd/74×cos35.5°＝9,150/74×0.814≒100lx

となります。

図3：光が斜めに入射する場合

光が斜めに入射する場合を示す図。光源の真下にある点P0から水平に5m離れた点P5が描かれている。光源から点P5の方向に向かう光線の鉛直角をθとし、θ方向の光線はIθ、点P5の水平面照度はEで表している。

2.直線光源による直接照度

直線光源Lの一端を含む垂直面内の点Pの直接照度は、下式で計算できます。

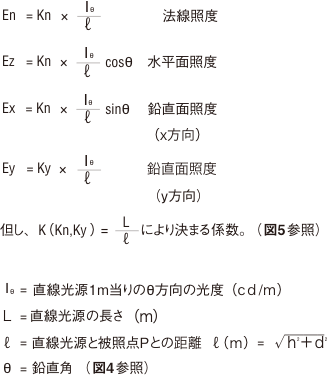
En＝Kn×Ⅰθ/ℓ 法線照度、Ez＝Kn×Ⅰθ/ℓcosθ 水平面照度、Ex＝Kn×Ⅰθ/ℓsinθ 鉛直面照度（ｘ方向）、Ey＝Ky×Ⅰθ/ℓ 鉛直面照度（ｙ方向）
但し、Ｋ（Ｋｎ、Ｋｙ）＝ L/ℓ により決まる係数。（図5参照）Ⅰθ＝直線光源1ｍ当りのθ方向の光度（ｃｄ/ｍ）、Ｌ＝直線光源の長さ（ｍ）、ℓ＝直線光源と被照点Ｐとの距離　ℓ（ｍ）＝ √‾‾̅ ｈの2乗＋ｄの2乗、θ＝鉛直角（図4参照）

図4：直線光源による照度

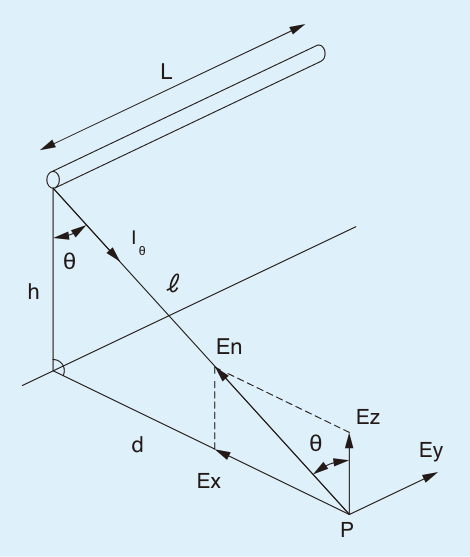
次の図のような一般的な場合は、光源L1、L2に分けて考えます。

図5：被照点が光源端を含む平面上にない場合

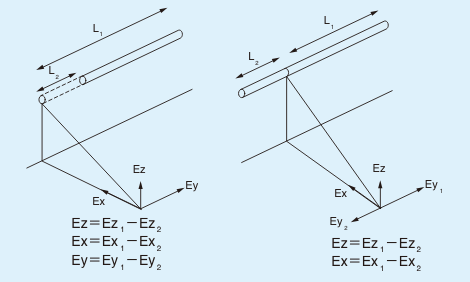
L1からL2の分短い場合：Ez=Ez1-Ez2、Ex=Ex1-Ex2、Ey=Ey1-Ey2、L1からL2の分長い場合：Ez=Ez1Ez2、Ex=Ex1-Ex2

【計算例】

直管形ランプ1灯用（ランプ光束3,400 lm）を、作業面上1.5m（=h）に取り付け、その中央直下より横へ1m（=d）離れた点Pの水平面照度EZはいくらになりますか？

（解）この場合の計算式は、

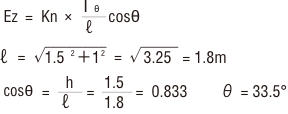
Ez＝Kn×Ⅰθ/ℓcosθ、ℓ＝√‾‾‾̅1.5の2乗＋1の2乗＝√‾‾3.25＝1.8m、cosθ＝h/ℓ＝1.5/1.8＝0.833　　θ＝33.5°

直線光源1m当りの33.5°方向の光度（Iθ）を求めるには、まず下記蛍光灯器具の配光曲線より、ランプ光束1,000 lm当りの光度（I’θ）を求めると

Ⅰ’θ= 207cd

次に、直管形ランプ1灯の1m当りの光束（F）は、長さ1.2mの時に3,400 lmですから

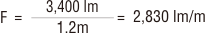
F＝3,400lm/1.2m＝2,830lm/m

となります。以上より

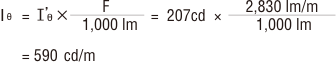
Ⅰθ＝Ⅰ’θ×F/1,000lm＝207cd×2,830lm/m/1,000lm＝590ｃｄ/m

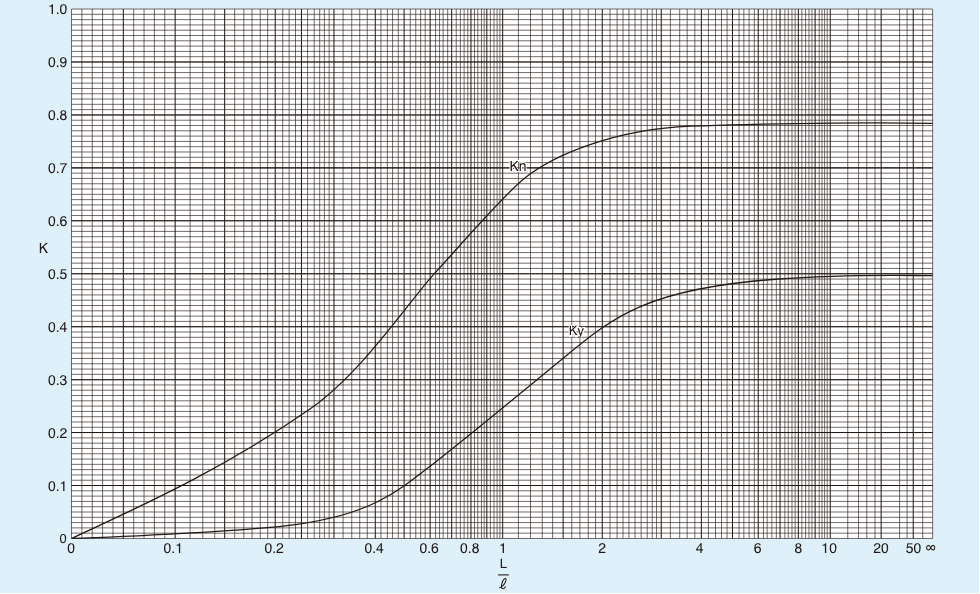
係数Knは

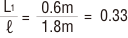
L1/ℓ＝0.6m/1.8m＝0.33

図表より Kn=0.31

故に照度E1は

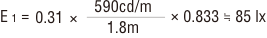
E1＝0.31× 590cd/m/1.8m×0.833≒85lx

E=E1+E2=85+85=170 lx

図6：直管形ランプの配光曲線

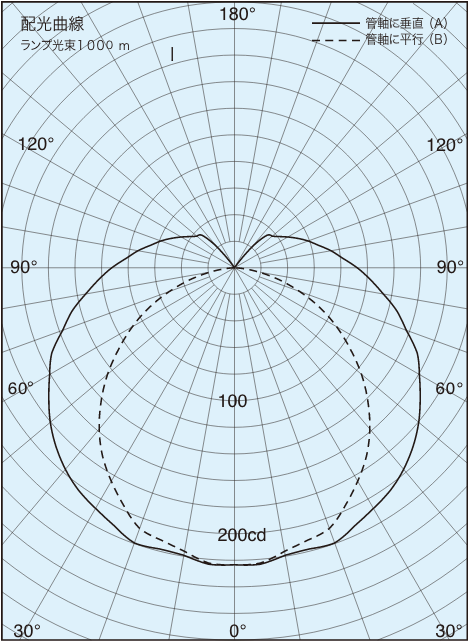
ランプ光束1,000 lmの配光曲線。中心から放射状に角度が描かれ、0°、30°、60°、90°、120°の範囲で配光が示されている。等照度線は100cd、200cdで描かれ、光束が角度に応じて分布している様子を示している。

図7：Knを求めるグラフ

横軸にL/ℓ、縦軸にKを取ったグラフ。KnとKyの2つの曲線が描かれており、どちらもL/ℓが4付近までは、L/ℓの値が大きくなるにつれてKの値も増加している。その後、L/ℓがさらに大きくなってもKの値は一定で変化しないことが示されている。

3.面光源による直接照度

（1）計算の向きが、面光源と直交する場合

（1）- 1 計算点が面光源の頂点にある場合

図8のように、輝度をL（cd/m²）とする完全拡散性の面光源（XxY）の一端から、距離Zだけ離れた場所の照度EZは、EZ=KpxLで求めます。

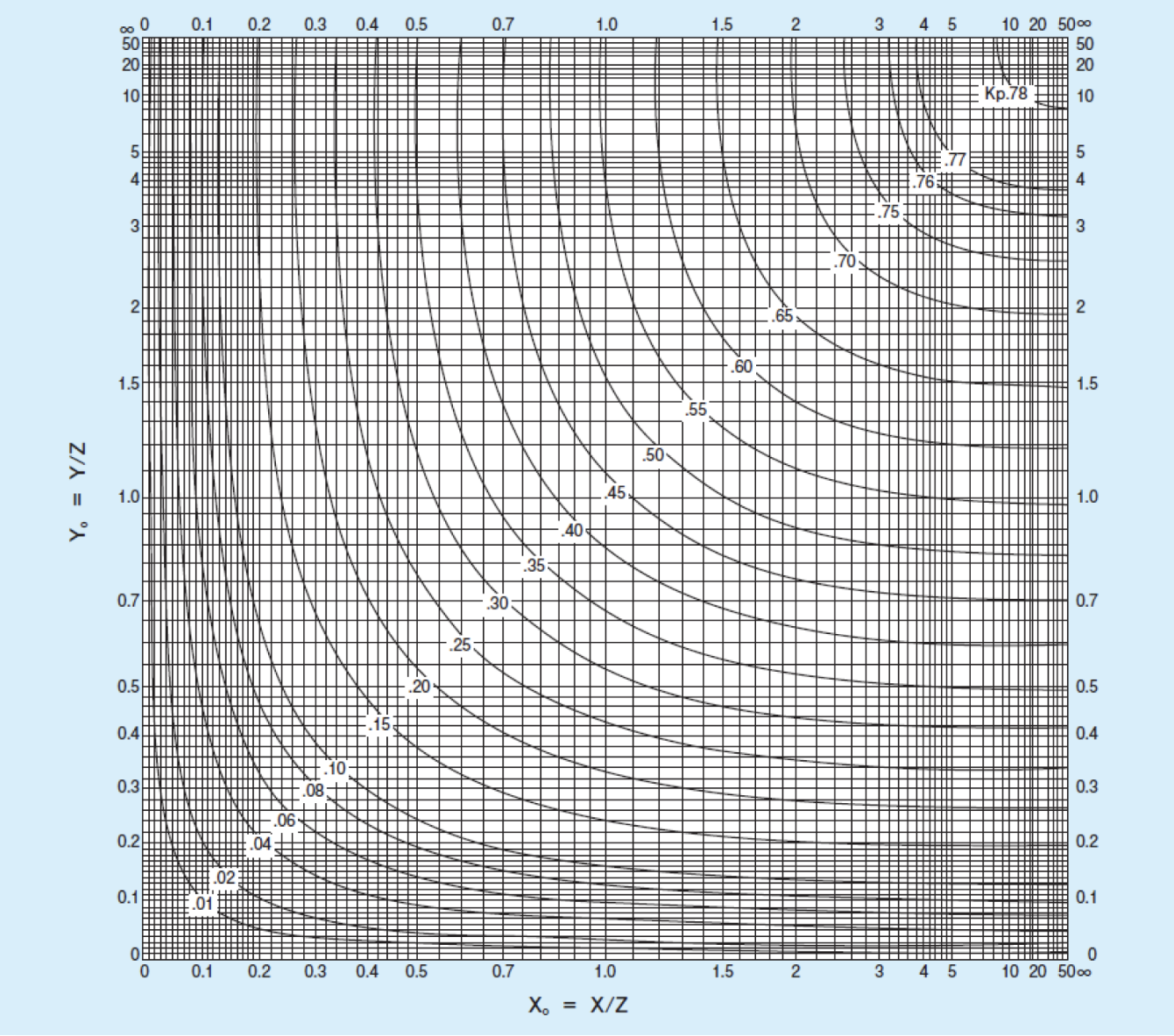
ここで、Kpは、まずXo=X/Z、Yo=Y/Zを求め、図9の横軸Xo、縦軸Yoの交点で得られるKpを導き、上の式でEZを求めます。

図8：計算の向きが面光源と直行で頂点の垂線にある場合

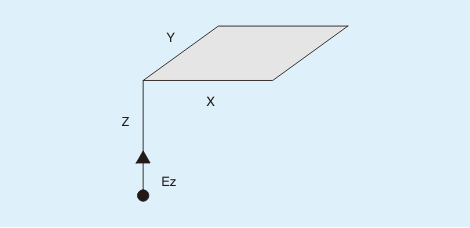
XY平面から垂直方向にZ軸だけ離れた位置にEzが示されている図。

図9：Kpを求めるグラフ

横軸にX0=X/Z、縦軸にY0=Y/Zを取ったグラフ。曲線上に、Kp.01、.02、.04、.06、.08、.10、.15、.20、.25、.30、.35、.40、.45、.50、.55、.60、.65、.70、.75、.76、.77、.78の値がそれぞれ示されている。

（1）- 2 計算点が面光源の頂点から離れている場合

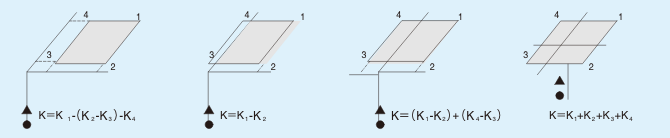
計算点が面光源の外や内になり、面光源の頂点から離れている場合は、図10に示したように、計算する面を2～4に分割し求めたKp値を、加減して導きます。

図10：計算点が頂点と離れている場合

面光源の頂点1234から34の外にある計算点の場合、K=K1-（K2-K3）-K4。面光源の頂点1234から34の少し内にある計算点の場合、K=K1-K2。面光源の頂点1234から12と34の真ん中付近にある計算点の場合、K=（K1-K2）+（K4-K3）。面光源の頂点1234の中心付近にある計算点の場合、K=K1+K2+K3+K4。

【計算例】

寸法が1.2mx1.2mの乳白パネルが、床上3mの天井に取り付けられています。乳白パネルは均一の完全拡散面と仮定し、輝度は2,000 cd/m²とします。乳白パネルの中央直下の水平面照度を導きます。

図10の右端の事例で、X=0.6m、 Y=0.6m、 Z=3mとなります。
Xo=X/Z=0.6/3=0.2、Yo= Y/Z=0.6/3=0.2であるから、図10においてKp=0.04を得ます。

EZ=KpxL=0.04x2,000=80 lx。これは、1/4の面積による照度であるから、80 lx x 4=320 lxとなります。

（2）計算の向きが、面光源と平行の場合

（2）- 1 計算点が面光源の頂点にある場合

図11のように、輝度をL（cd/m²）とする完全拡散性の面光源（XxY）の頂点から、距離Zだけ離れた場所の照度Eyは、Ey=KvxLで求めます。

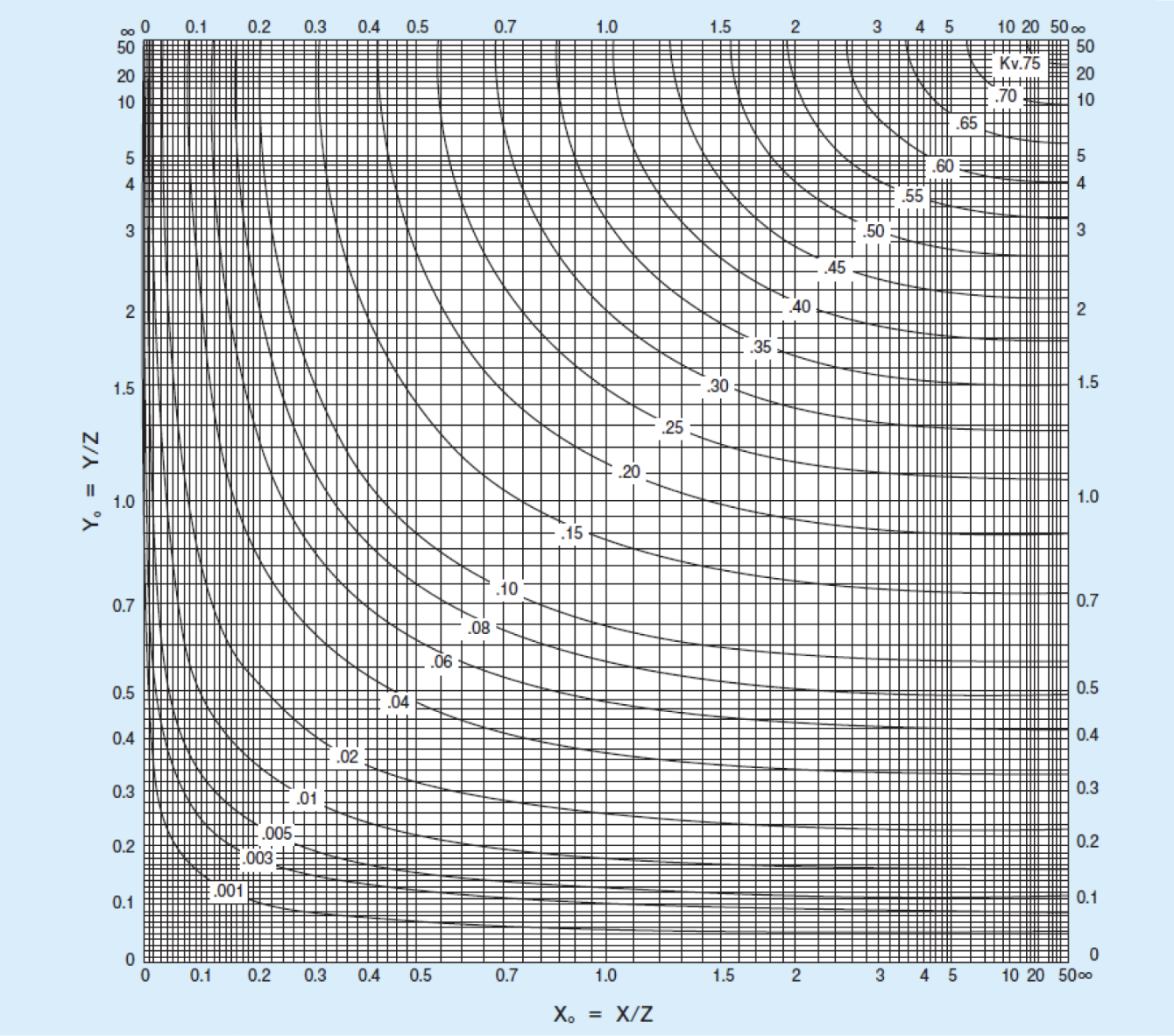
ここで、Kvは、Xo=X/Z、Yo= Y/Zを求め、図12より導きます。

図11：計算の向きが面光源と平行で頂点の垂線にある場合

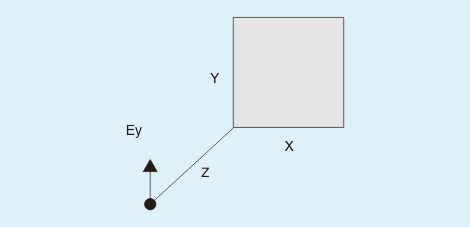
XY平面からZだけ離れた場所の照度Eyを示した図。

図12：Kvを求めるグラフ

横軸にX0=X/Z、縦軸にY0=Y/Zを取ったグラフ。曲線上に、Kp.001、.003、.005、.01、.02、.04、.06、.08、.10、.15、.20、.25、.30、.35、.40、.45、.50、.55、.60、.65、.70、.75の値がそれぞれ示されている。

（2）- 2 計算点が面光源の頂点から離れている場合

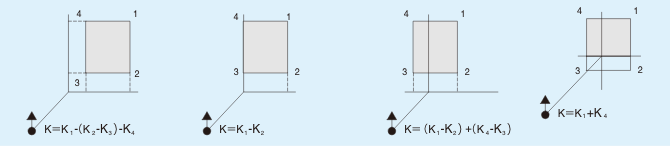
計算点が、面光源の外や内になり、面光源の頂点と離れている場合は、図13に示したように、分割し、Kvを加減して導きます。

図13：計算点が頂点と離れている場合

面光源の頂点1234から34の外にある計算点の場合、K=K1-（K2-K3）-K4。面光源の頂点1234から23の外にある計算点の場合、K=K1-K2。面光源の頂点1234から14と23の真ん中付近にある計算点の場合、K=（K1-K2）+（K4-K3）。面光源の頂点1234の中心付近にある計算点の場合、K=K1+K4。

【計算例】

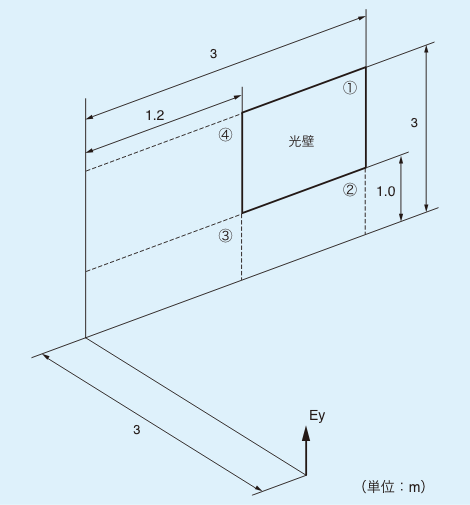
光壁からの光による水平面照度を導きます。

図13の左端の事例で説明します。光壁、計算点の条件は図14に示します。光壁輝度は、5,000cd/m²とします。

① 点

x/z=3/3=1y/z=3/3=1Kv1=0.17

② 点

x/z=3/3=1y/z=1/3=0.33Kv2=0.035

③ 点

x/z=1.2/3=0.4y/z=1/3=0.33Kv3=0.017

④ 点

x/z=1.2/3=0.4y/z=3/3=1Kv4=0.09

Ey=Lx（Kv1-（Kv2-Kv3）- Kv4）=
5,000cd/m²x（0.17-（0.035-0.017）-0.09）=
310 lx

図14：光壁による照度計算事例

印刷はこちらから

関連ページ

ルミナスプランナー

ルミナスプランナー

簡易な操作で平均照度の算出、照度分布図を作成。

照明設計事例 LIGHITING STYLE

照明設計事例
LIGHTING STYLE

パナソニックが照明設計に携わった物件について、照明計画手法、プロセス、ノウハウをご紹介。

施設・部位別モデルプラン

施設・部位別モデルプラン

オフィスや学校など施設毎の特徴に合わせた、照明のモデルプラン。

パナソニックの電気設備のSNSアカウント